Trong thực tế, tính toán trong không gian nhiều chiều của các hàm phức tạp (chẳng hạn trong EM là tính posterior và kỳ vọng của nó) là rất khó khăn nên người ta dùng phương pháp xấp xỉ.

10.1 Variational Inference

Kí hiệu set của N i.i.d data là $\mathbf{X}=\{x_ 1, \ldots, x_ n\}$, tất cả latent variables là $\mathbf{Z}=\{z_ 1, \ldots, z_ n\}$. Mô hình của chúng ta sẽ là joint distribution $p(\mathbf{X},\mathbf{Z})$, và mục tiêu là đi tìm giá trị xấp xỉ cho posterior distribution $p(\mathbf{Z}|\mathbf{X})$ và model evidence $p(\mathbf{X})$.

Từ chương trước khi nói về EM, ta có chỉ ra rằng:

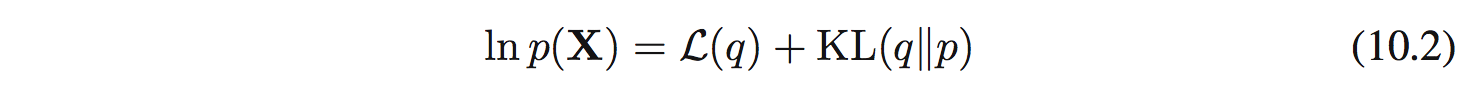
ở đây:

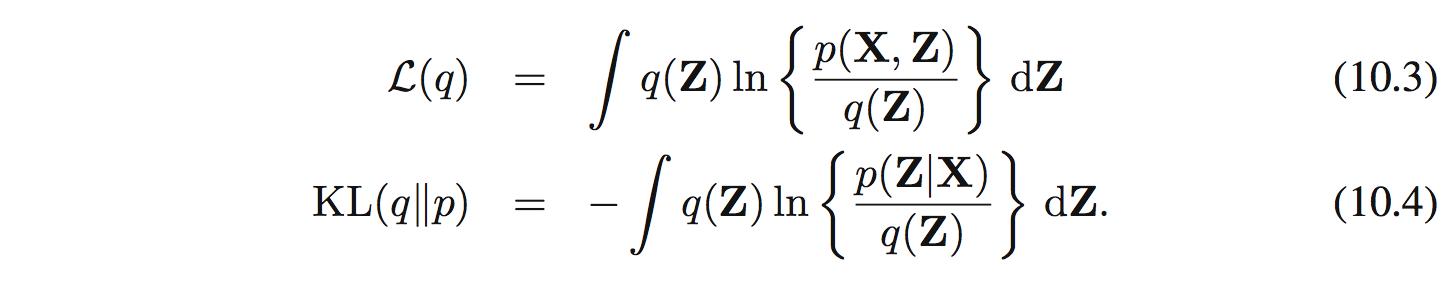
Để tìm $q(\mathbf{Z})$ ta có thể ràng buộc theo 1 họ phân phối nào đó. Cách khác để xấp xỉ là dùng phương pháp như miêu tả dưới đây:

10.1.1 Factorized distributions

Giả sử có thể phân tích $\mathbf{Z}$ thành các nhóm không giao nhau $\mathbf{Z}_ i$ với $i=1,\ldots,M$. Giả sử phân phối q có thể phân tích được thành như sau:

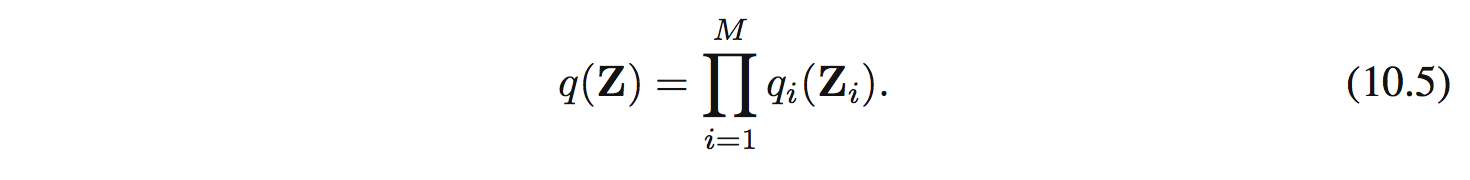
Giờ cần tìm các $q_ i$ để lower bound $\mathcal{L}(q)$ là lớn nhất. Chú ý là ở đây ta không hề có ràng buộc nào đối với $q_ i$.

Thay (10.5) vào (10.3):

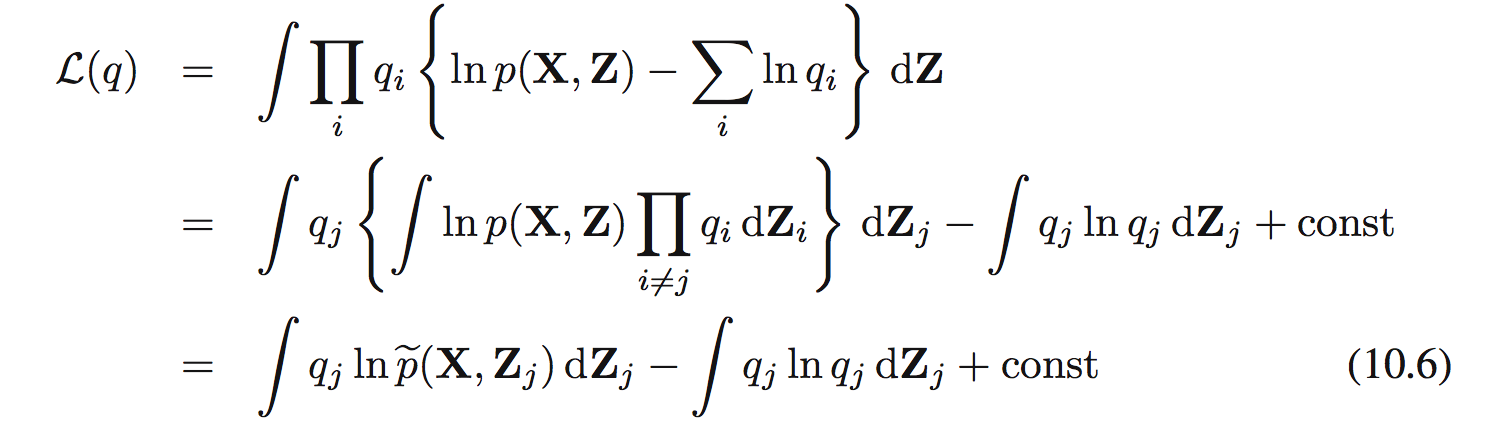
Ở đây:

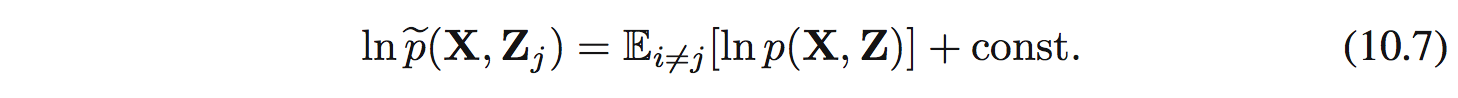
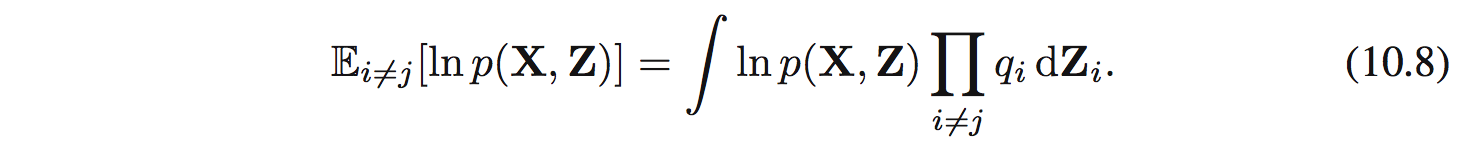
Dễ dàng nhận thấy (10.6) là negative KL divergence giữa $q_ j(\mathbf{Z}_ j)$ và $\hat{p}(\mathbf{X},\mathbf{Z}_ j)$. Tìm max của (10.6) sẽ tương đương với tìm min của KL và nó sẽ xảy ra khi $q_ j(\mathbf{Z}_ j) = \hat{p}(\mathbf{X},\mathbf{Z}_ j$. Tức là ta sẽ tìm được optimal solution $q^{*}_ j(\mathbf{Z} _j)$:

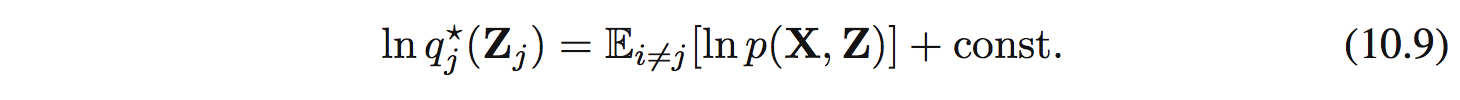
10.1.2 Properties of factorized approximations

Để hiểu về tính chất của phương pháp factorized approximation, ta thử xấp xỉ 1 Gaussian bằng 1 factorized Gausian.

Giả sử có 1 Gaussian $p(\mathbf{z}) = \mathcal{N}(\mathbf{z}|\mathbf{\mu},\mathbf{\Lambda}^{-1}$ với $\mathbf{Z}=(z1,z2)$ và:

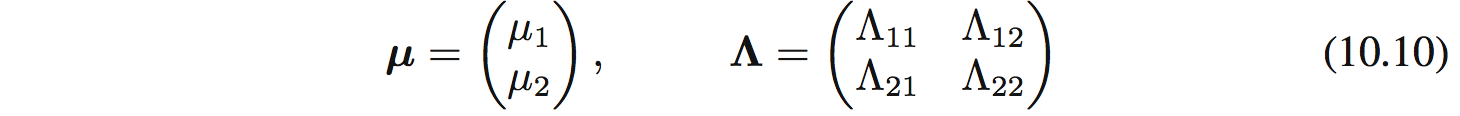
Ở đây thì $\Lambda_ {21}=\Lambda_ {12}$. Giờ ta muốn tìm xấp xỉ phân phối này bằng factorized Gaussian $q(\mathbf{z}) = q_ 1(z_ 1)q_ 2(z_ 2)$.

Sử dụng công thức (10.9) ta được:

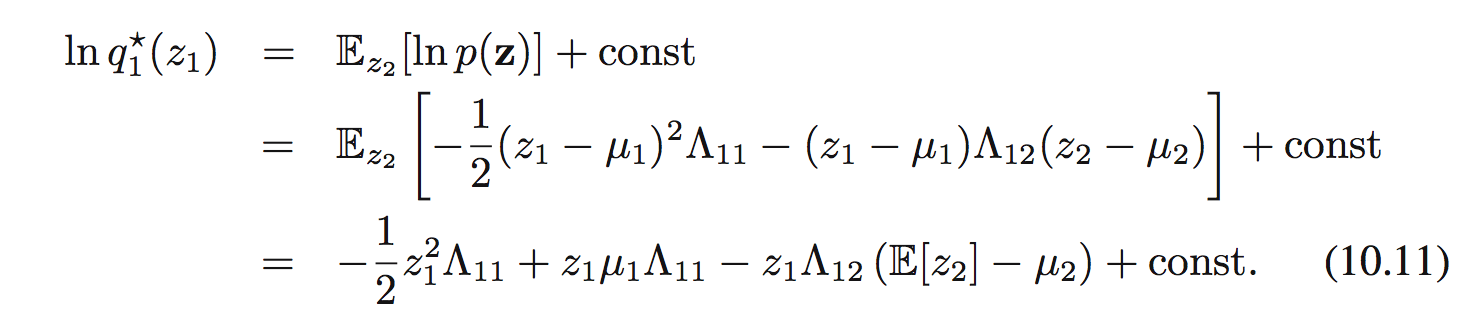
Để ý là vế phải là 1 hàm bậc 2 đối với $z_ 1$ nên ta có thể chỉ ra được $q^{*}(z_ 1)$ là 1 Gaussian. Chú ý là ta không hề giả sử $q(z_ i)$ là Gaussian mà tìm được nó theo tính toán.

Bằng việc so sánh 2 vế, ta sẽ tìm được mean và precision của Gaussian này:

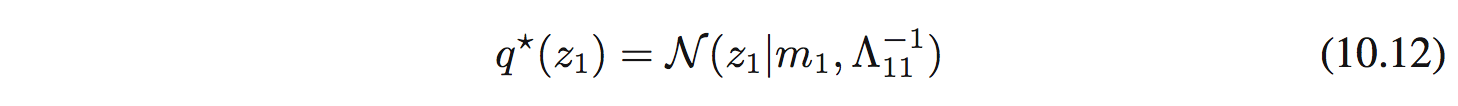với

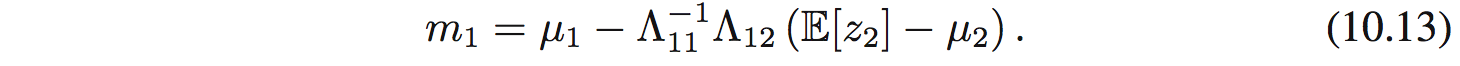
Vì tính đối xứng, $q^*_ 2(z_ 2)$ cũng là 1 Gaussian:

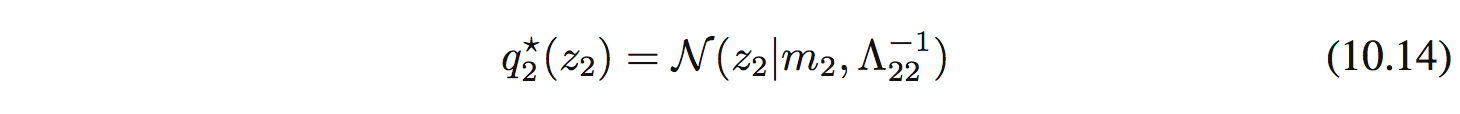với

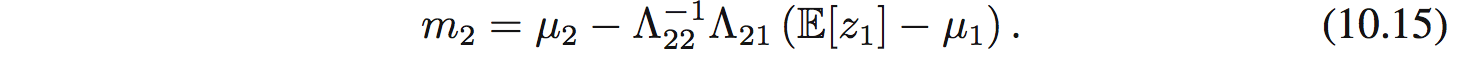
$q^*(z_ 1)$ tính dựa vào $q^*(z_ 2)$ và ngược lại. Nên ta sẽ phải tính đi tính lại cho đến khi hội tụ.

Để ý là $\mathop{{}\mathbb{E}}[z_ 1] = \mu_ 1$ và $\mathop{{}\mathbb{E}}[z_ 2] = \mu_ 2$ sẽ là 1 nghiệm. Kết quả này biểu thị ở hình 10.2a. Để ý là mean thì chính xác nhưng variance thì bị co về chiều nhỏ hơn.

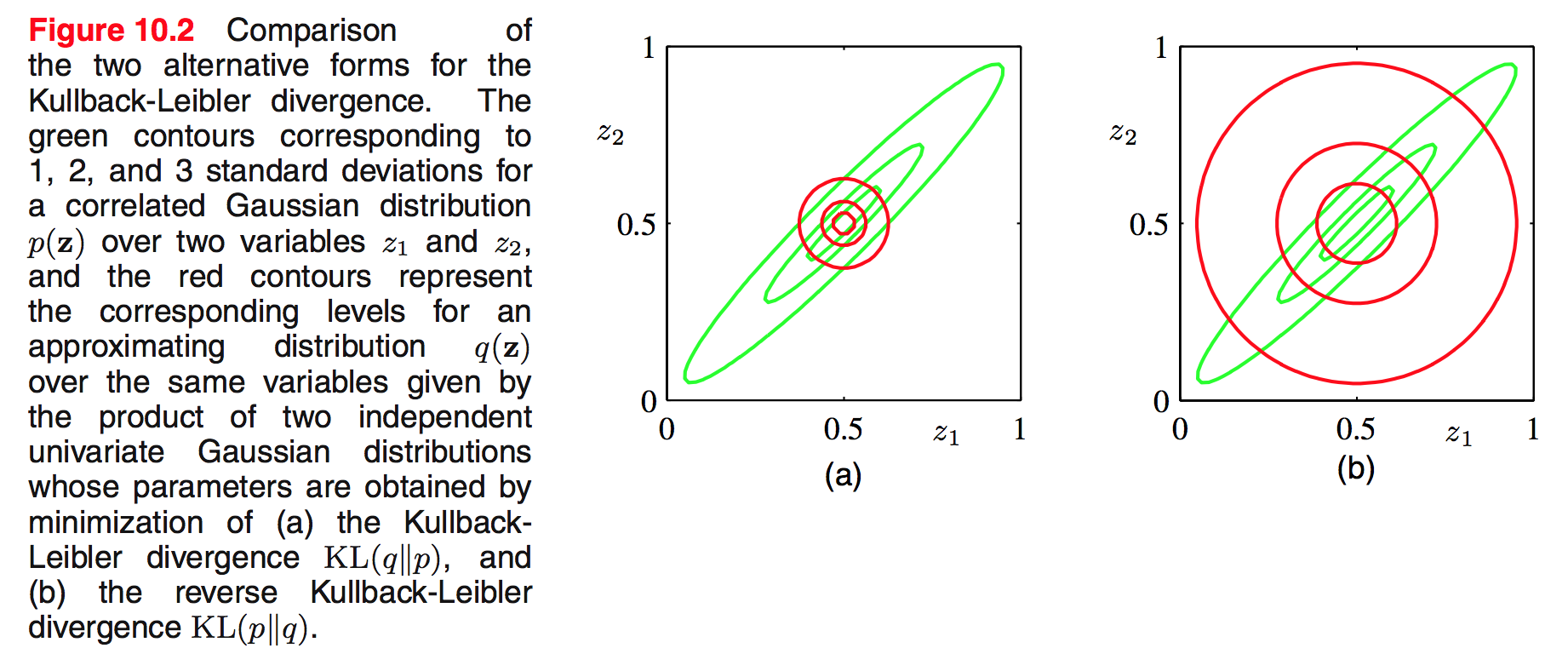
Để so sánh thì ta xét việc tìm min của reverse KL divergence KL(p||q). Kết quả tìm được biểu thị ở hình 10.2b. Mean tìm được cũng chính xác nhưng variance lại bị phình ra.

Nhân tiện nói về KL, ta so sánh sự khác biệt của việc tìm min KL(p||q) và min KL(q||p) trong bài toán dùng 1 Gaussian để xấp xỉ 1 mixture của 2 Gaussian như hình vẽ dưới đây:

10.1.3 Example: The univariate Gaussian

Giờ bài toán là factorized variational approximation sử dụng 1 Gaussian theo 1 biến $x$. Mục tiêu là tìm posterior cho mean $\mu$ và precision $\tau$, được cho bởi data set $\mathcal{D} = \{x_ 1,\ldots, x_ N\}$ được lấy độc lập từ 1 Gaussian.

Hàm likelihood là:

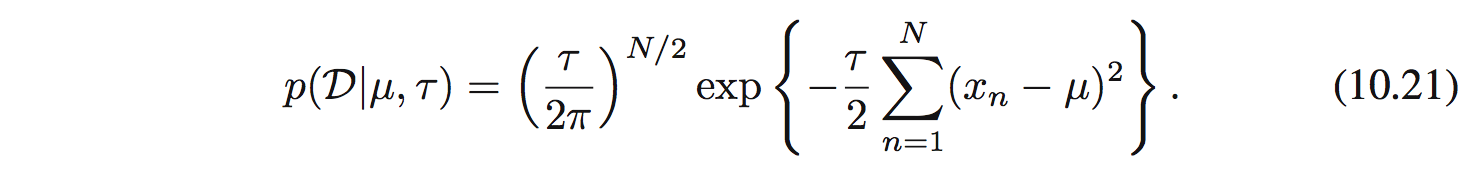
Conjugate prior đối với $\mu$ và $\tau$ được cho bởi:

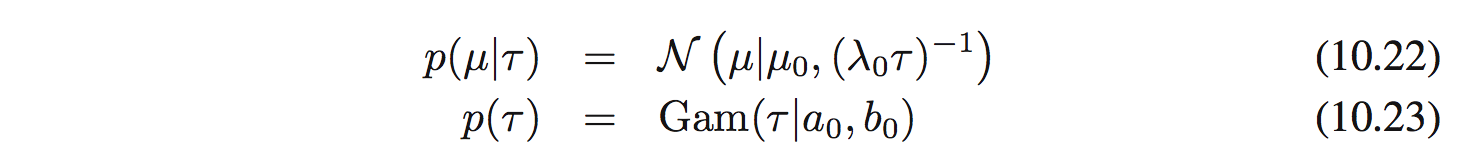
Đối với bài toán đơn giản này có thể tìm được posterior 1 cách chính xác nhưng với mục đích tutorial ta thử xấp xỉ nó bằng factorized variational approximation:

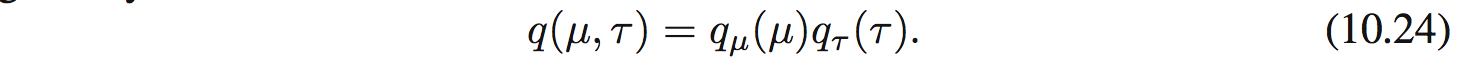
Từ công thức (10.9) ta tìm được:

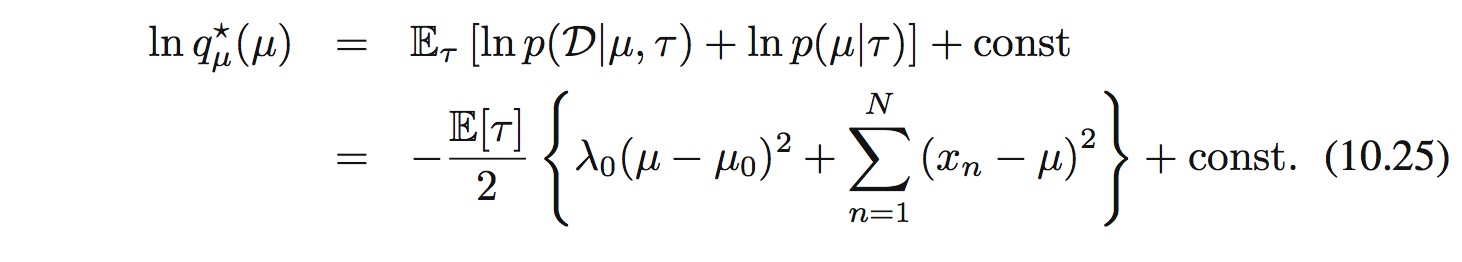
Ta thấy là $q_ \mu(\mu)$ là 1 Gaussian $\mathcal{N}(\mu|\mu_ N, \lambda_ N^{-1}$ với mean và precision là:

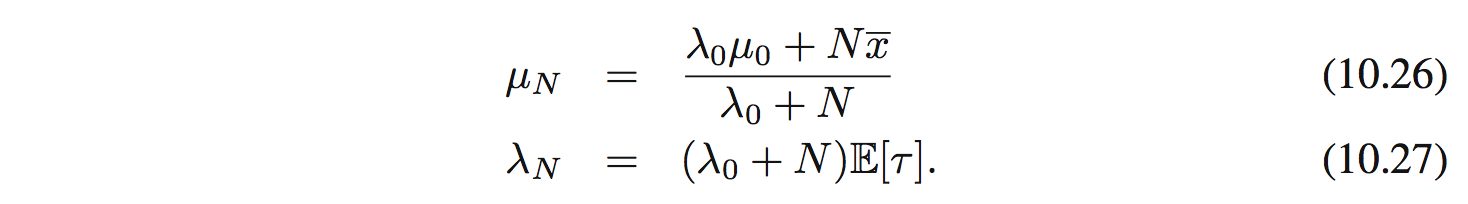
Để ý là khi $N \rightarrow \infty$ sẽ cho kết quả của maximum likelihood là $\mu_ N = \bar{x}$ và precision là vô cùng.

Tương tự tìm $q_ \tau (\tau)$:

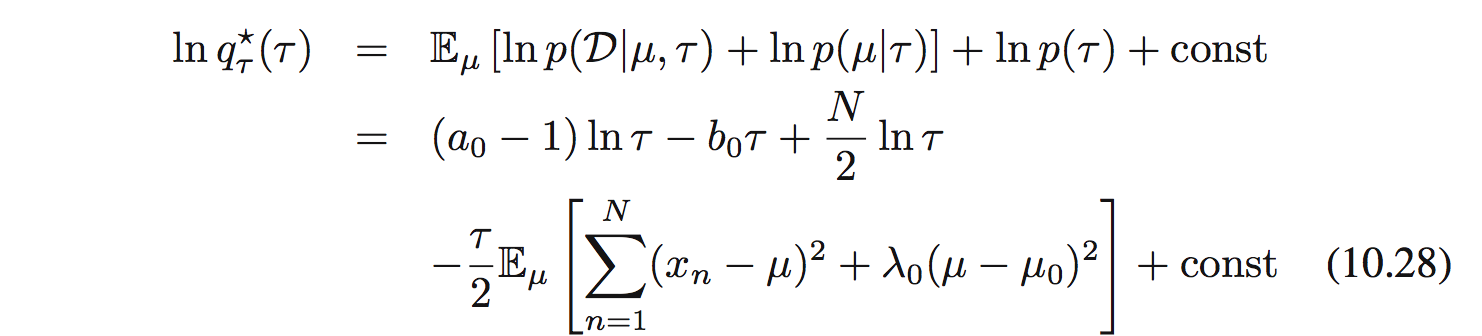
và $q_ \tau (\tau)$ là phân phối gamma $\mathrm{Gam}(\tau|a_ N, b_ N)$:

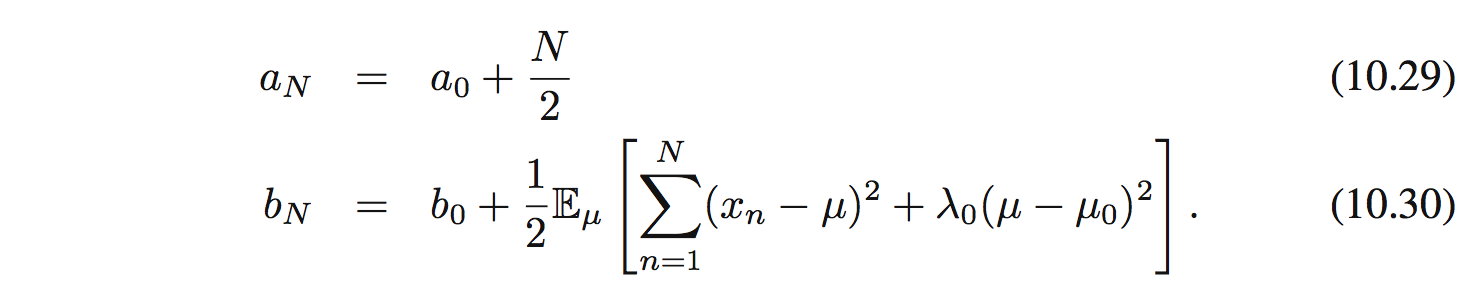
Biểu hiện cũng tương tự khi $N \rightarrow \infty$.

• PRML
• Vietnamese