Bài toán là tìm kỳ vọng của hàm $f(z)$ đối với phân phối $p(z)$:

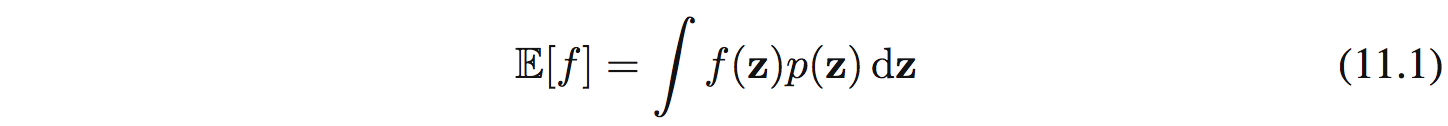
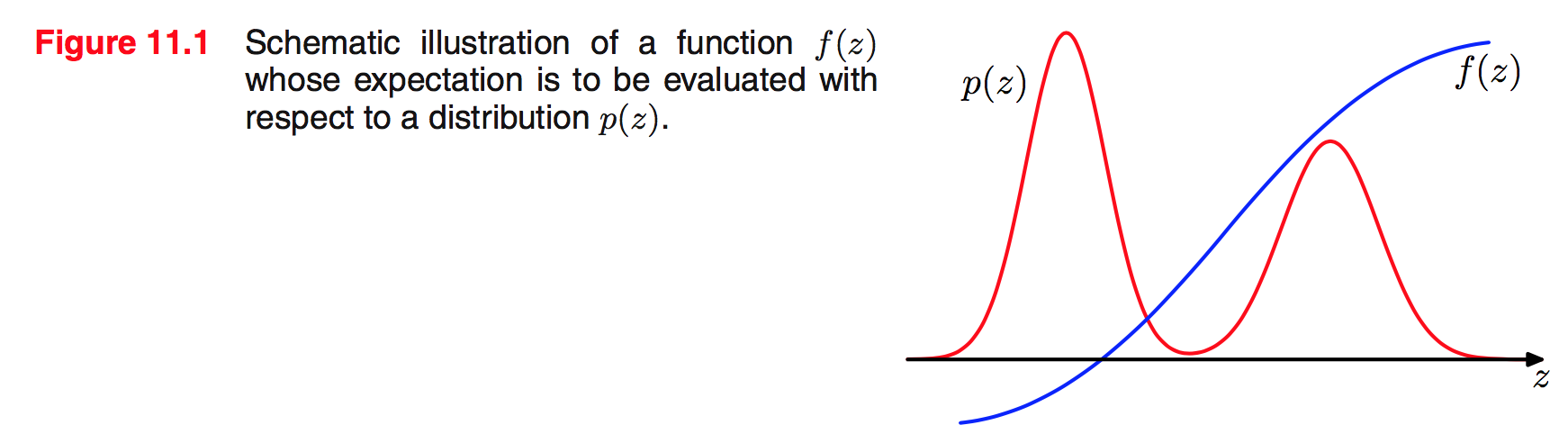
Ta xét bài toán là giá trị kỳ vọng này rất khó để tính bằng giải tích trực tiếp.

Ý tưởng để giải bài này là lấy các giá trị $z^{(l)} (l=1,\ldots, L)$ độc lập từ phân phối $p(z)$. Khi đó, công thức (11.1) sẽ được xấp xỉ thành tổng của các giá trị rời rạc:

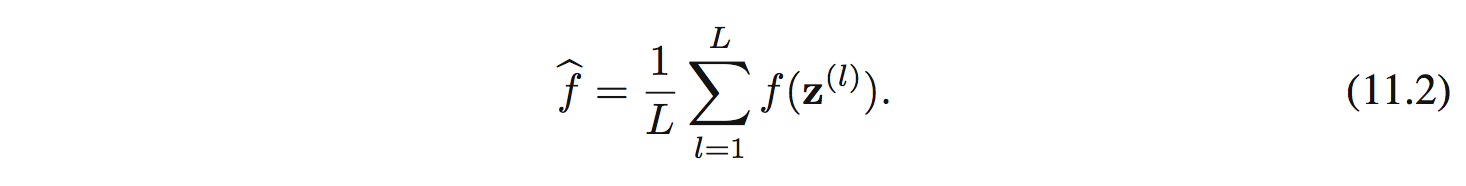
Giá trị trung bình có kỳ vọng chính xác nhưng phương sai sẽ là:

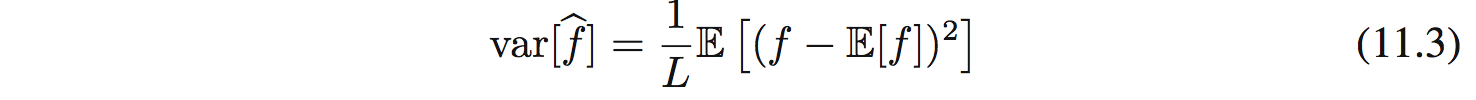
Thêm 1 vấn đề trong thực tế là các giá trị $z^{(l)} (l=1,\ldots, L)$ có thể không độc lập với nhau.

Basic Sampling Algorithms

Ở phần này, ta sẽ đề cập các phương pháp sampling.

Standard distributions

Các phần mềm máy tính đều dễ dàng sampling (pseudo-random) phân phối đều trong khoảng (0,1). Ta sử dụng kết quả này để sampling 1 vài phân phối đơn giản khác.

Giả sử $z$ tuân theo phân phối đều trong khoảng (0,1). $y=f(z)$ là 1 hàm số, thì phân phối $p(y)$ sẽ trở thành:

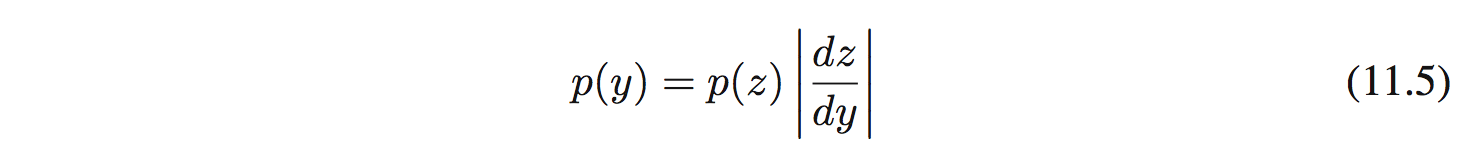
Trong trường hợp này $p(z)=1$. Lấy tích phân lên sẽ được:

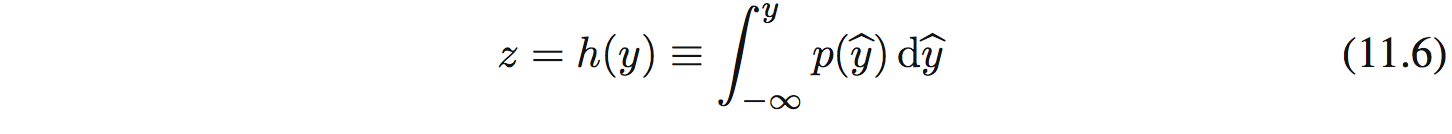
Cuối cùng ta sẽ được $y=h^{-1}(z)$.

Ví dụ phân phối mũ:

$$ p(y) = \lambda \exp(-\lambda y) $$

Sử dụng công thức sẽ được:

$$ y = -\lambda^{-1}\ln (1-z) $$

11.1.2 Rejection sampling

Giờ thì $p(z)$ không phải dạng cơ bản nên không làm được theo phương pháp trên. Giả sử có hàm $\tilde{p}(z)$ mà:

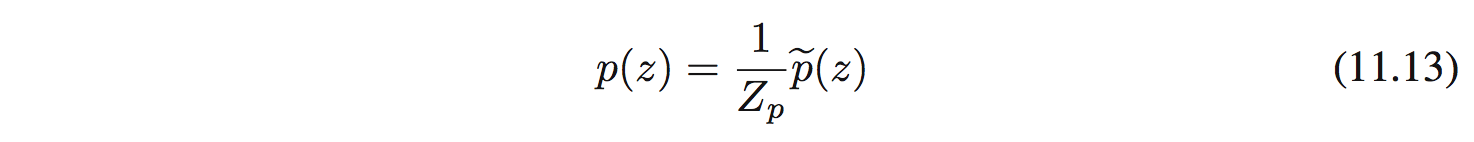
ở đây $\tilde{p}(z)$ có thể đánh giá được nhưng $Z_ p$ thì chưa biết.

Thêm nữa có 1 phân phối đơn giản $q(z)$. Phương pháp sampling biểu diễn ở hình sau:

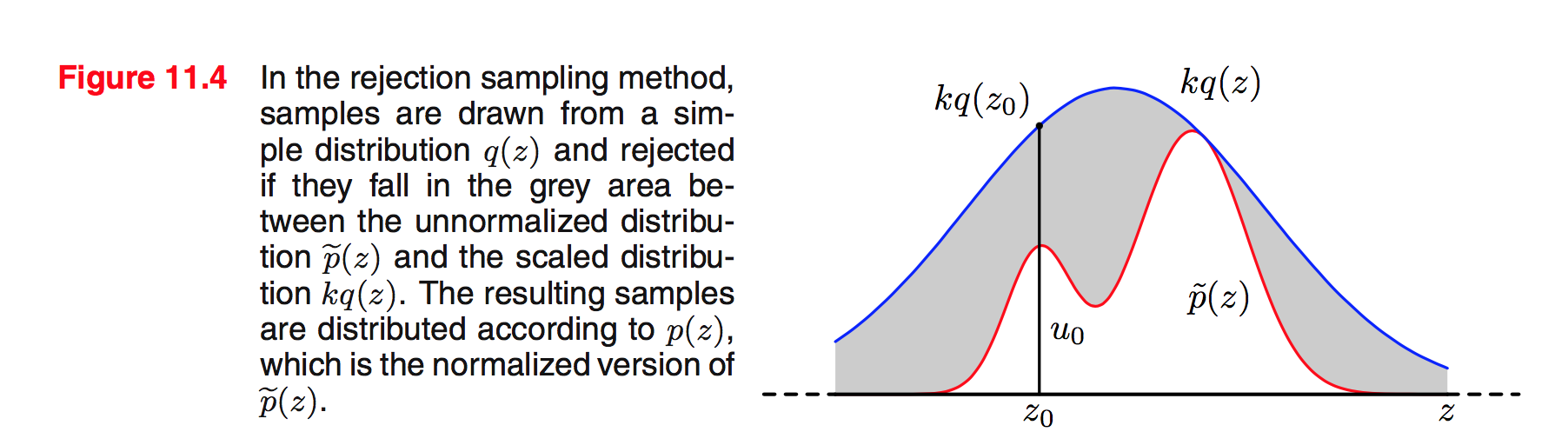
Công thức sẽ là:

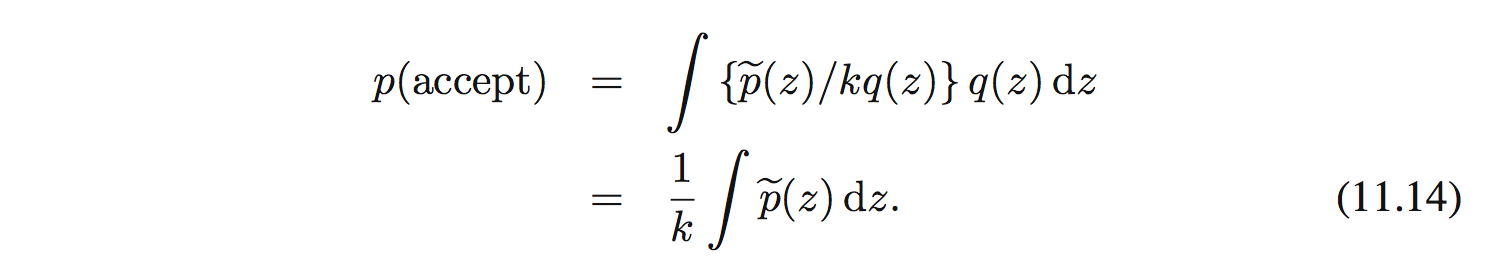
11.1.3 Adaptive rejection sampling

Hàm $q(z)$ chọn ngẫu nhiên như trên thì tỉ lệ reject cao. Nên ta dùng phương pháp cập nhật dần như sau: