PRML - Chap 12: Continuous Latent Variables - 12.2.3 ~ end
By Huy Van
12.2.3 Bayesian PCA
Graphical model cho Bayesian PCA được biểu diễn như sau:

Ở đây ta đã đưa thêm Gaussian prior độc lập cho $\mathbf{W}$ với các precision $\alpha_i$:
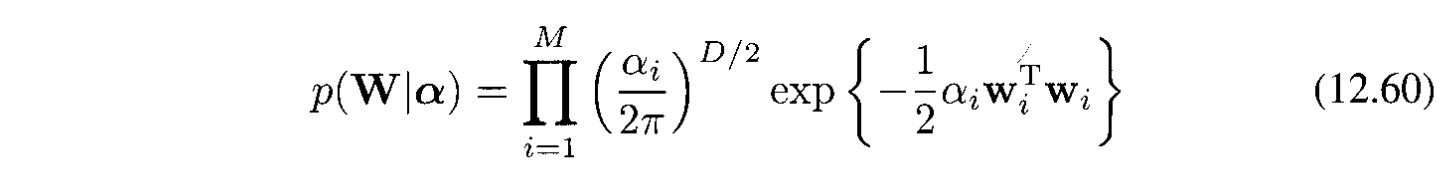
Giá trị của $\alpha_i$ được tìm bằng cách maximizing the maginal likelihood:
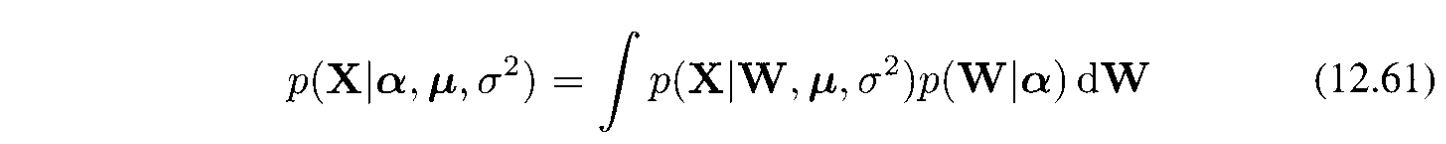
Chú ý là để đơn giản ở đây ta coi $\mathbf{\mu}$ và $\sigma^2$ là các parameters chứ không đưa thêm priors cho chúng.
Sử dụng Laplace approximation, các $\alpha_i$ sẽ tìm được như sau:
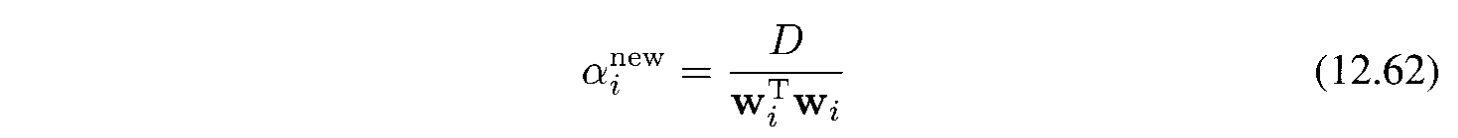
như theo công thức (3.98). Ở đây $D$ là số chiều của $\mathbf{w}_i$.
Còn lại thì sử dụng EM hoàn toàn tương tự như phần 12.2.2.
12.2.4 Factor analysis
Factor analysis là 1 linear-Gaussian latent variable model rất gần với probabilistic PCA, chỉ khác ở chỗ conditional distribution của observed variable $\mathbf{x}$ cho bởi latent variable $\mathbf{z}$ có covariance dạng diagonal thay vì isotropic:
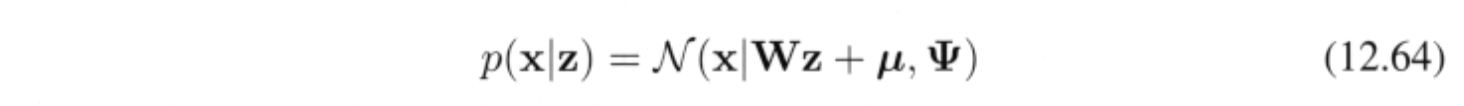
với $\Psi$ là $D \times D$ diogonal matrix.
Sử dụng (2.115), ta tính được marginal distribution cho observed variable $p(x)=\mathcal{N}(x|\mathbf{\mu},\mathbf{C})$ với $\mathbf{C}=\mathbf{W}\mathbf{W}^T + \mathbf{\Psi}$.
Tìm parameters $\mathbf{\mu}$,$\mathbf{W}$ và $\mathbf{\Psi}$ bằng maximum likelihood. Solution $\mathbf{\mu}$ sẽ là sample mean. Tuy nhiên ta không tìm được closed-form solution cho $\mathbf{W}$. Nhưng có thể tính bằng EM. Cụ thể, E-step:
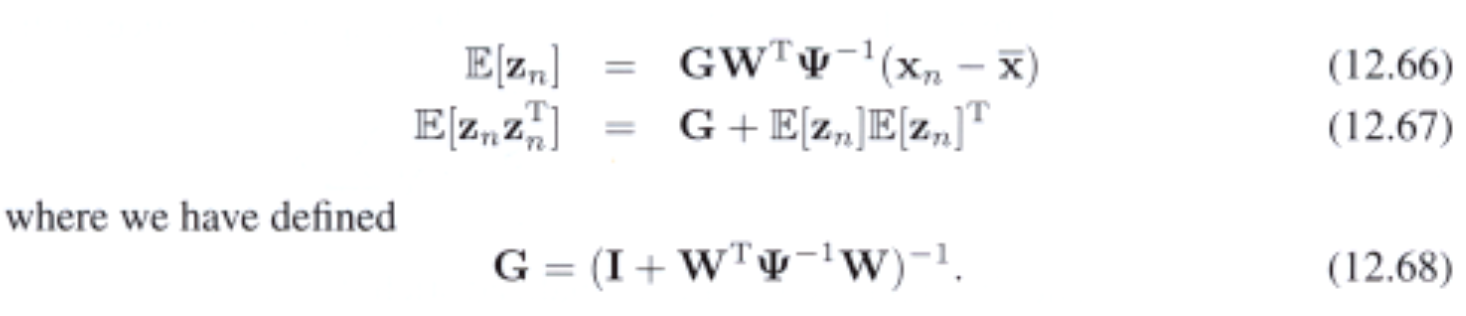
M-step:
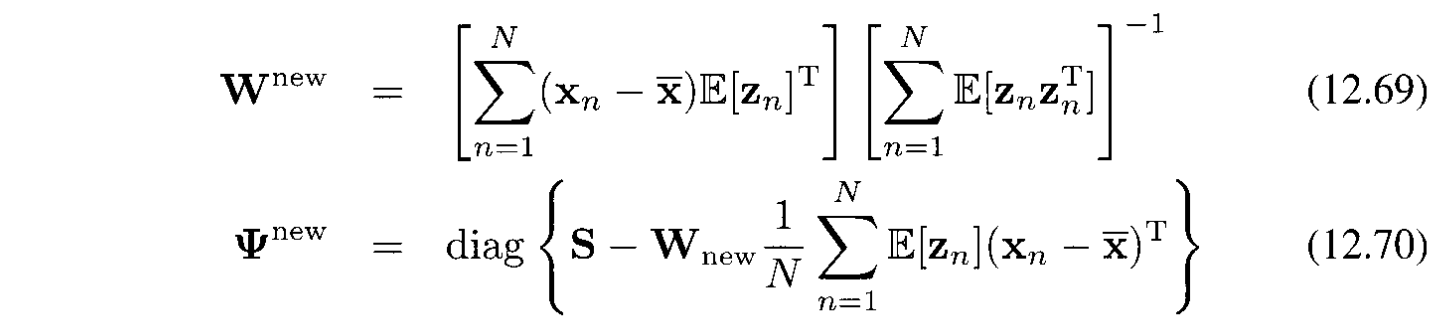
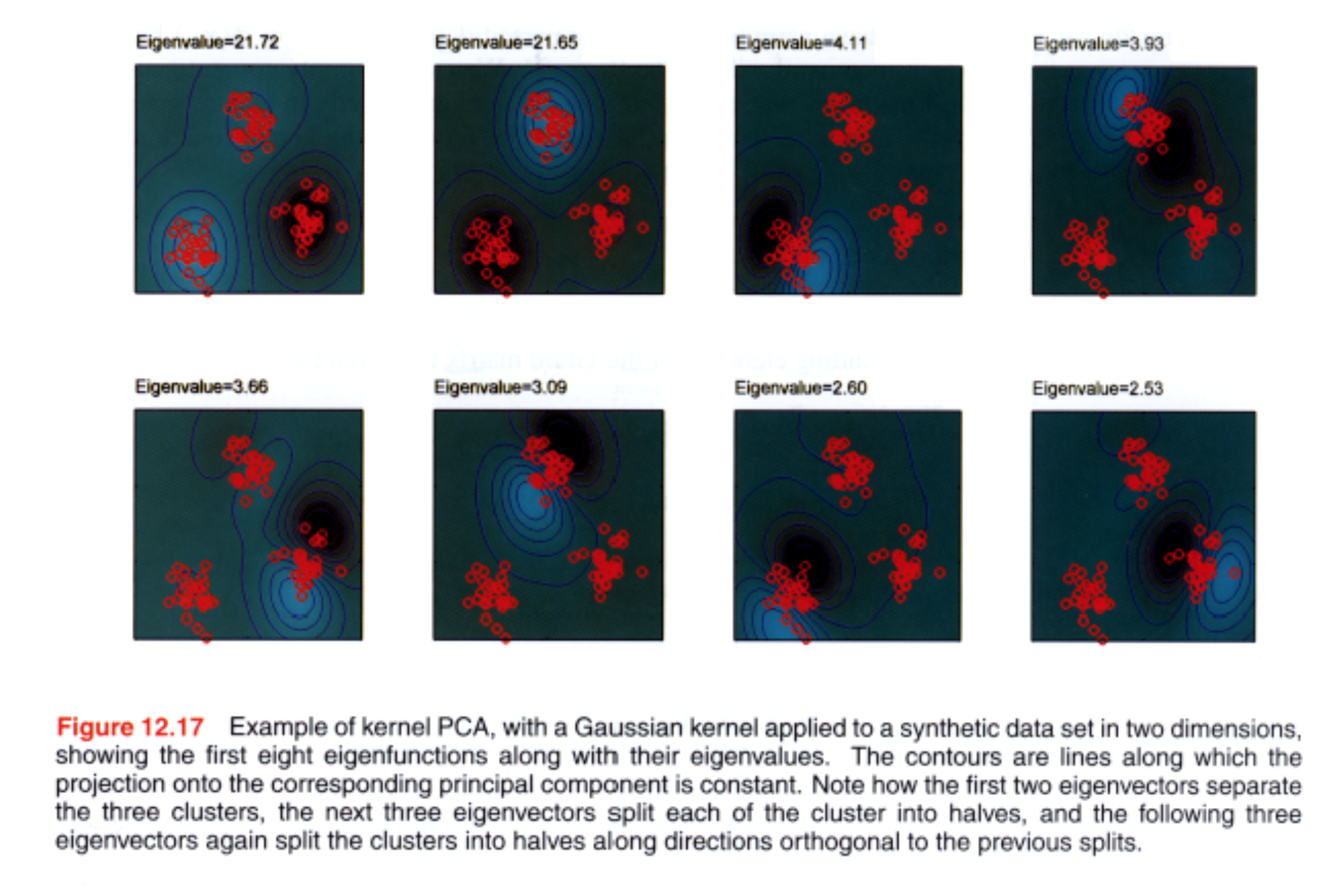
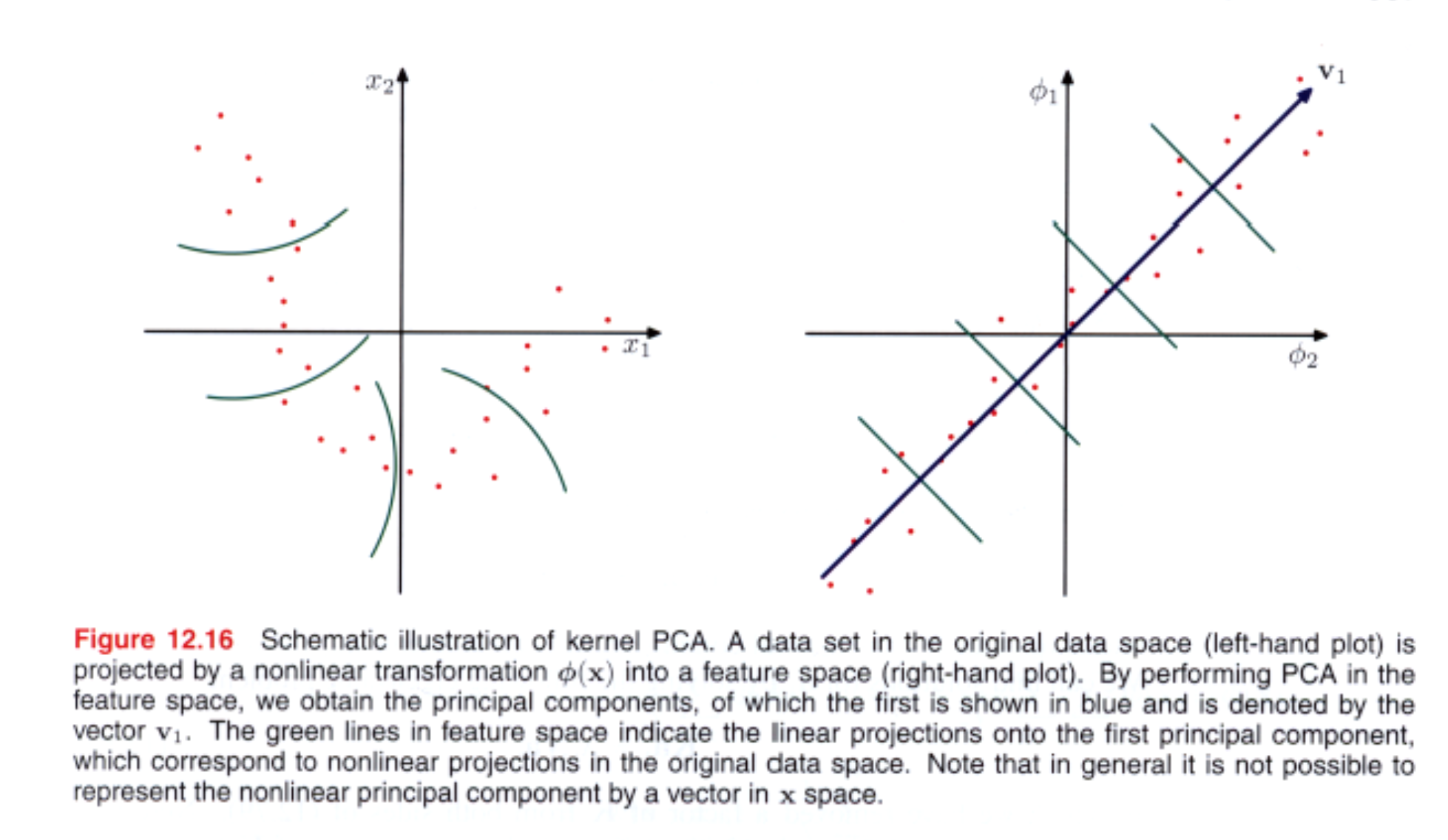
12.3 Kernel PCA
Ở chương 6 ta đã nhìn thấy kỹ thuật thay thế kernel cho scalar product $x^Tx’$. Giờ tìm cách làm tương tự cho PCA.
Có data set $\{x_ n \}$ với $n=1,\ldots,N$ trong không gian có số chiều là $D$. Để đơn giản ta giả sử ta đã trừ các vector $x_ n$ cho sample mean để được $\sum_ n x_ n = 0$. Nhơ lại là principal components được định nghĩa bởi vector riêng $\mathbf{u}_ i$ của covariance matrix:
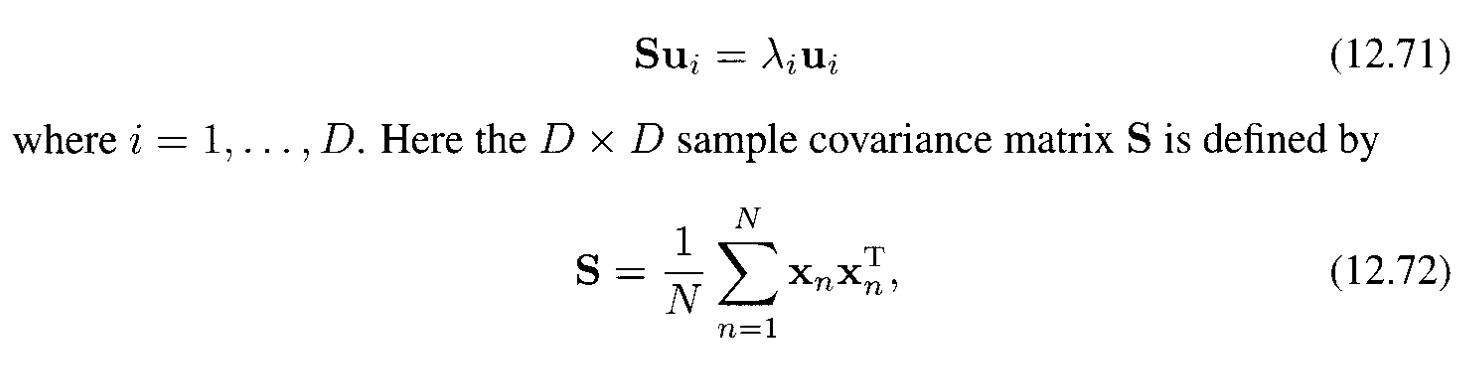
và các vector riêng được normalized để $\mathbf{u}_ i^T \mathbf{u}_ i = 1$.
Giờ coi 1 phép biến đổi phi tuyến $\phi(x)$ tới không gian M chiều, sao cho mỗi data point $x_ i$ được chiếu thành $\phi(x_ n)$.
Giả sử là data sau khi chiếu cũng có mean là 0 tức là $\sum_ n \phi(x_ n) = 0$. $M \times M$ sample covariance matrix sẽ là:
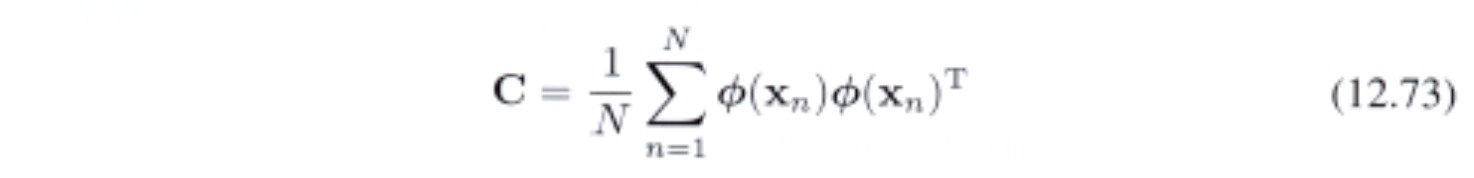
và vector riêng của nó được định nghĩa bởi:
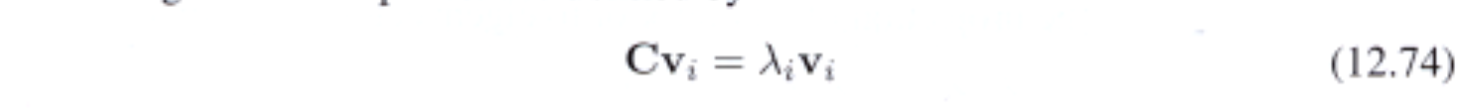
với $i=1,\ldots,M$. Mục tiêu của chúng ta là tìm giá trị riêng này. Từ định nghĩa của $\mathbf{C}$, $v_ i$ phải thoả mãn:

Thay vào phương trình vector riêng ta được:
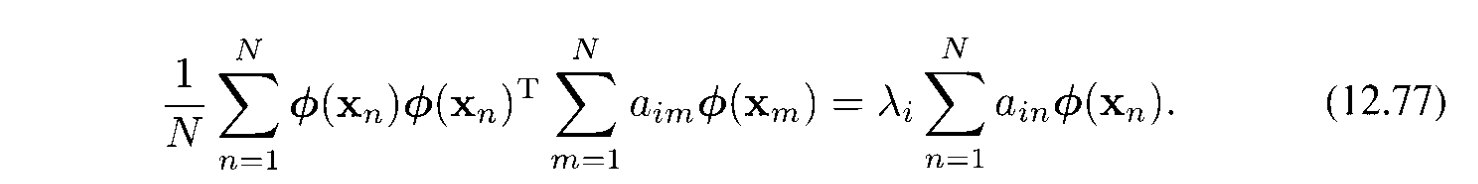
Bước chính là biểu diễn cái trên thành kernel function $k(x_ n, x_ m) = \phi(x_ n)^T\phi(x_ m)$ bằng cachs nhân 2 vế với $\phi(x_ l)^T$ để được:
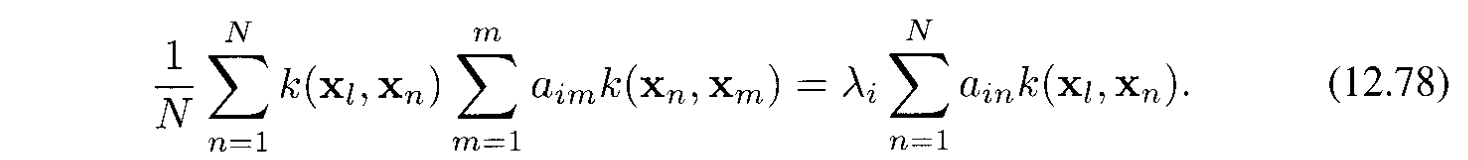
Viết lại bằng ký hiệu matrix:
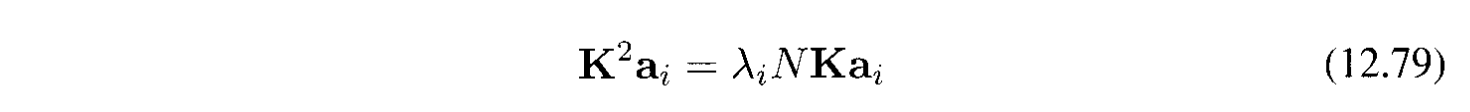
Bỏ $\mathbf{K}$ ở cả 2 vế:
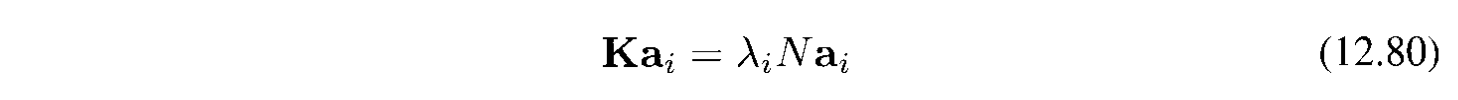
Điều kiện normalization cho hệ số $\mathbf{a}_ i$ yêu cầu là vector riêng cũng phải được normalized. Sử dụng (12.76) và (12.80) ta đươc:
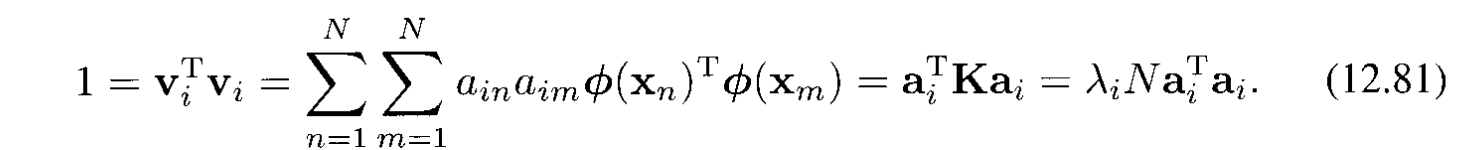
Sử dụng (12.76) hình chiếu của điểm $x$ trên vector riêng $i$ là:
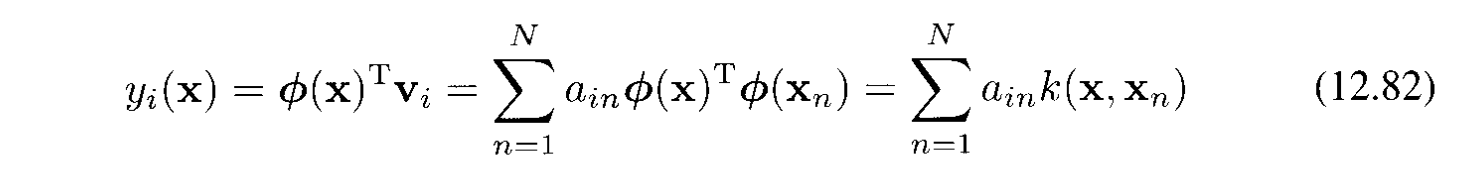
Cái này cũng được biểu diễn theo kernel function.
Trên đây ta đã biểu diễn được projected data set cho bởi $\phi(x_ n)$ có zero mean. Cho trường hợp tổng quát, ký hiệu là $\tilde{\phi}(x_ n)$:
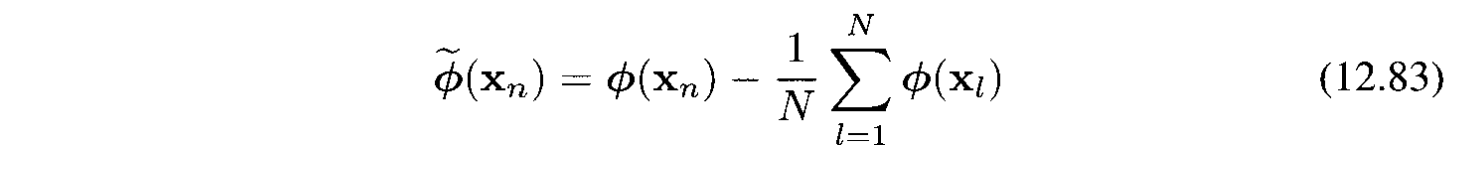
và Gram matrix:
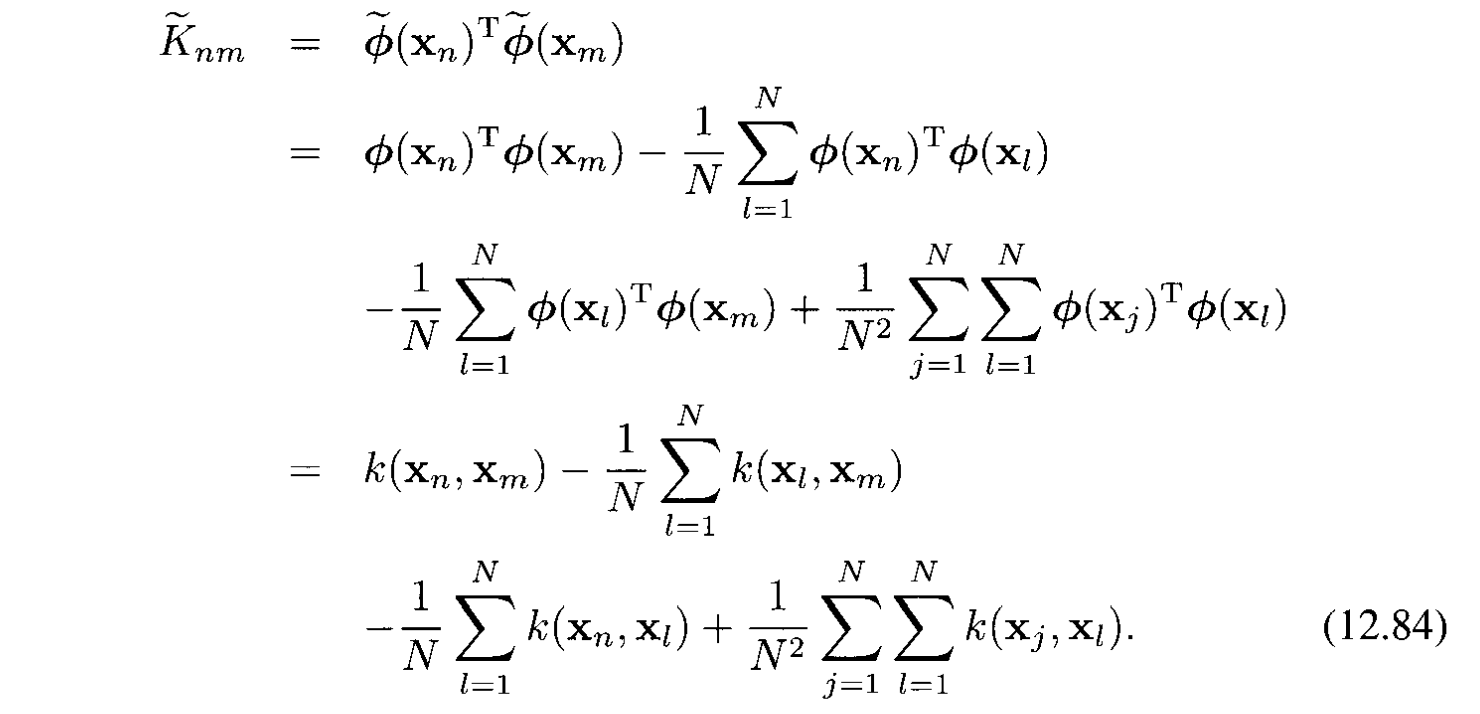
Đổi sang ký hiệu matrix sẽ được:
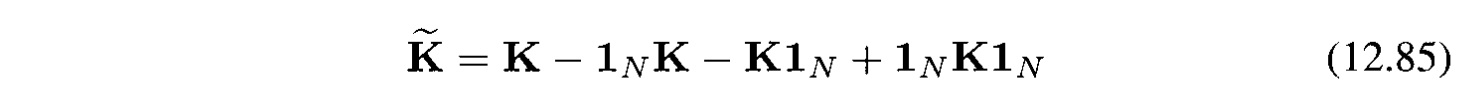
với $\mathbf{1}_ N$ là $N \times N$ matrix mà mỗi phần tử đều là $1/N$.