PRML - Chap 7: Sparse Kernel Machines 7.1.1 ~ 7.1.3

By Huy Van

7.1.1 Overlapping class distributions

Trong phần trước chúng ta đã giả sử là dữ liệu rất đẹp và tồn tại đường biên giới có thể chia được các class ra tách biệt với nhau. Tuy nhiên trong thực tế thì vì dữ liệu có noise nên nếu cố tìm đường biên giới để tách các class thì dễ dẫn đến overfit. Trong phần này, chúng ta sẽ xây dựng model mà cho phép 1 vài điểm có thể bị phân loại sai, vì mục đích chính là model chạy tốt trên tập test. Phương pháp này còn gọi là soft margin. Chúng ta giới thiệu thêm biến mới gọi là slack varibles $\xi_n \ge 0$ với $n=1,\ldots,N$ ($N$ là số điểm trong training data).

  • $\xi_n = 0$ nếu điểm được phân loại đúng
  • $\xi_ n = | t_ n - y(x_ n)|$ nếu điểm bị phân loại sai

Ở đây $x_ n$ là input, $y(x_ n)$ là output của model ($y(\mathbf{x})=\mathbf{w}^T\phi(x)+b$, $>0$ thì thuộc 1 class, $<0$ thì thuộc class còn lại, $=0$ nếu nằm trên đường biên giới), còn $t_ n$ là label (luôn có giá trị $1$ hoặc $-1$). Để ý là giá trị $\xi_ n$ càng lớn nếu điểm bị phân loại sai $x_ n$ càng xa đường biên giới.

Tóm lại:

  • $\xi_ n = 0$ nếu điểm được phân loại đúng.
  • $0< \xi_ n \le 1$ thì điểm sẽ nằm trong 2 đường biên, nhưng vẫn được phân loại đúng.
  • $\xi_ n=1$ nếu $x_ n$ nằm trên đường biên giới (tức là $y(x_ n) = 0$).
  • $\xi_ n > 1$ nếu bị phân nhầm class.

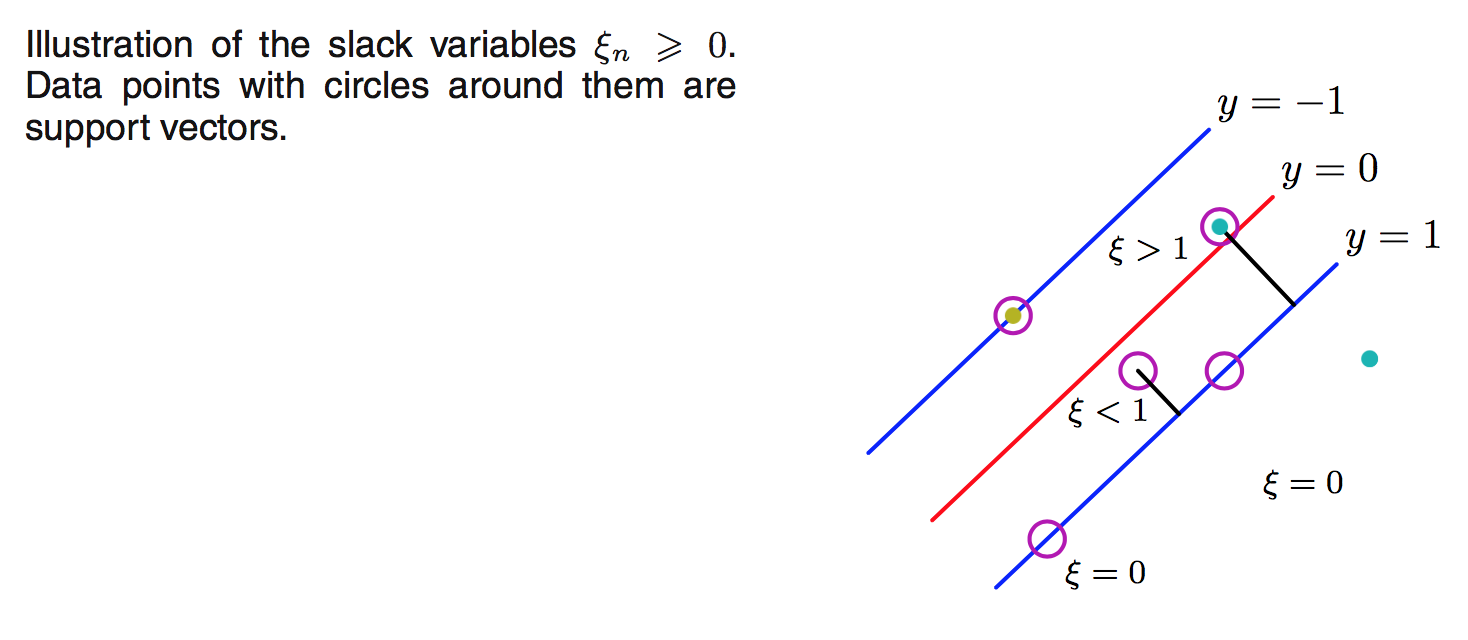figure-7.3 (Hình này hơi khó nhìn, các bạn tham khảo hình 7.3 trong sách cho chính xác.)

Nhớ lại ở phần trước, tất cả các điểm đều phải thoả mãn điều kiên:

$$ t_ n y(x_ n) \ge 1 $$

và minimize $$ \frac{1}{2}||w||^2 $$

thì ở đây điều kiện này trở thành:

$$ t_ n y(x_ n) \ge 1 - \xi_ n \\ \xi_ n \ge 0 $$

và minimize

$$ C\sum_ {n=1}^N \xi_n + \frac{1}{2}||w||^2 \tag{7.21} \label{eq:7.21} $$

Ở đây $C>0$ là tham số điều khiển trade-off giữa slack variable penalty và margin.

Để giải bài toán tìm min với điều kiện ràng buộc thì ta dùng phương pháp nhân tử Lagrange. Hàm Lagrangian sẽ là:

$$ \begin{align} L(\mathbf{w},b,\mathbf{\xi},\mathbf{a},\mathbf{\mu}) &= \frac{1}{2} ||\mathbf{w}||^2+C\sum_ {n=1}^{N}\xi_ n \\ & - \sum_ {n=1}^{N} a_ n \{t_ n y(x_ n) -1 + \xi_ n \} \\ & - \sum_ {n=1}^{N} \mu_ n \xi_ n \end{align} $$

với $\{a_ n \ge 0\}$ và $\{\mu_ n \ge 0\}$ là các nhân tử Lagrange.

Tập điều kiện KKT của Lagrangian này là:

$$ \begin{align} a_ n & \ge 0 \tag{7.23} \label{eq:7.23}\\ t_ n y(x_ n) -1 + \xi_ n & \ge 0 \tag{7.24} \label{eq:7.24}\\ a_ n (t_ n y(x_ n) -1 + \xi_ n) & = 0 \tag{7.25} \label{eq:7.25}\\ \mu_ n & \ge 0 \tag{7.26} \label{eq:7.26}\\ \xi_ n & \ge 0 \tag{7.27} \label{eq:7.27}\\ \mu_ n \xi_ n & = 0 \tag{7.28} \label{eq:7.28}\\ \end{align} $$

Giờ ta giải bài toán này bằng việc lấy vi phân đối với từng biến thì sẽ được:

$$ \begin{align} \frac{\partial L}{\partial \mathbf{w}} = 0 \quad & \Rightarrow \quad \mathbf{w} = \sum_ {n=1}^N a_ n t_ n \phi(x_ n) \tag{7.29} \label{eq:7.29} \\ \frac{\partial L}{\partial b} = 0 \quad & \Rightarrow \quad \sum_ {n=1}^N a_ n t_ n = 0 \tag{7.30} \label{eq:7.30}\\ \frac{\partial L}{\partial \xi_ n} = 0 \quad & \Rightarrow \quad a_ n = C - \mu_n \tag{7.31} \label{eq:7.31} \end{align} $$

Khử $\mathbf{w}, b$ và $\{\xi_ n\}$ ở Lagrangian ta quy được về bài toán maximize 1 hàm bậc 2 đối với $\{a_ n\}$ như sau:

$$ \tilde{L}(\mathbf{a}) = \sum_ {n=1}^{N} a_ n -\frac{1}{2} \sum_ {n=1}^{N}\sum_ {m=1}^{N} a_ n a_ m t_ n t_ m k(x_ n, x_ m) \tag{7.32} \label{eq:7.32} $$

Chú ý ở đây là $a_ n \ge 0$, $\mu_ n \ge 0$ nên từ $\eqref{eq:7.30}, \eqref{eq:7.31}$ ta suy ra điều kiện đối với $\{a_ n\}$ như sau:

$$ 0 \le a_ n \le C \\ \sum_ {n=1}^N a_ n t_ n = 0 $$

Đối với 1 giá trị mới của $x$, sử dụng $\eqref{eq:7.29}$ ta có thể phân loại nó dựa theo:

$$ y(x) = \sum_ {n=1}^N a_ n t_ n k(x, x_n) + b \tag{7.13} \label{eq:7.13} $$

Phương trình này giống với phần trước (không có $\xi$).

Nhận xét 1 chút về kết quả.

  • Với $a_ n = 0$ thì giá trị này không đóng góp vào kết quả $\eqref{eq:7.13}$.
  • Với $a_ n > 0$ thì từ $\eqref{eq:7.25}$ ta có $t_ n y(x_ n) = 1 - \xi_ n$. Các điểm này được gọi là support vectors.
    • Nếu $a_ n < C$ thì từ $\eqref{eq:7.31}$ ta có $\mu_ n > 0$ nên thay vào $\eqref{eq:7.28}$ sẽ được $\xi_ n = 0$. Nghĩa là điểm này sẽ nằm trên đường biên.
    • Nếu $a_ n = C$ thì điểm này sẽ nằm trong 2 đường biên, và có thể được phân loại đúng (khi $\xi _n \le 1$) hay phân loại nhầm (khi $\xi _n > 1$).

Giờ ta đi tìm giá trị của $b$ trong $\eqref{eq:7.13}$. Để ý là với các suport vectors có $0 < a_ n < C$ thì $\xi_ n = 0$ nên $t_ n y(x_ n) =1 $, vì thế:

$$ t_ n \Big( \sum_ {m \in S} a_ m t_ m k(x_ n, x_ m) + b \Big) = 1 $$

Ta sẽ tìm được 1 giá trị ổn định của $b$ bằng việc sử dụng $t_ n^2 = 1$ và lấy trung bình các giá trị là:

$$ b = \frac{1}{N_ M} \sum_ {n \in M} \Big( t_ n - \sum_ {m \in S} a_ m t_ m k(x_ n, x_ m) \Big) $$

Ở đây $S$ là tập toàn bộ support vectors, $M$ là tập gồm các support vectors có $0 < a_ n < C$.

Có 1 phương pháp tương tự Support Vector Machine đã trình bày ở đây là ν-SVM. Thay vì $\eqref{eq:7.32}$ thì ta maximize hàm sau đây:

$$ \tilde{L}(\mathbf{a}) = -\frac{1}{2} \sum_ {n=1}^{N}\sum_ {m=1}^{N} a_ n a_ m t_ n t_ m k(x_ n, x_ m) \tag{7.38} \label{eq:7.38} $$

với điều kiện là:

$$ 0 \le a_ n \le 1/N \\ \sum_ {n=1}^N a_ n t_ n = 0 \\ \sum_ {n=1}^N a_ n \ge \nu $$

Vì hàm $\eqref{eq:7.21}, \eqref{eq:7.13}$ là hàm bậc 2 (quadratic) nên nếu tồn tại cực trị (local optimum) thì điểm đó sẽ là global optimum. Tuy nhiên việc tìm giá trị chính xác trong thực tế là khó khăn do giới hạn tính toán và memory nên người ta sử dụng kỹ thuật như là chunking, decomposition method, hay sequential minimal optimization (SMO).

7.1.2 Relation to logistic regression

Nhớ lại về logistic regression (chương 4.3.2) với $t \in \{0,1\} $ thì:

$$ p(t|y) = (\sigma(y))^t (1-\sigma(y))^{1-t} $$

Nếu ta chuyển $t \in \{-1,1\}$ thì chú ý rằng $$ p(t=1|y)=\sigma(y) \\ p(t=-1|y)=1-\sigma(y)=\sigma(-y) $$ với $\sigma(y)$ là hàm logistic sigmoid $\sigma(y) = \frac{1}{1+\exp(-y)}$.

Vì thế:

$$ p(t|y) = \sigma(yt) $$

Cross entropy error với regularizer sẽ được viết lại thành:

$$ \begin{align} E & = -\ln p(\mathbf{t}|\mathbf{y}) + \lambda||\mathbf{w}||^2 \\ & = \sum_ {n=1}^N E_ {LR}(y_ n t_ n) + \lambda||\mathbf{w}||^2 \end{align} $$

với $E_ {LR}(yt) = \ln(1+\exp(-yt))$

Trở lại với SVM, mục tiêu là minimze \eqref{eq:7.21}:

$$ C\sum_ {n=1}^N \xi_n + \frac{1}{2}||\mathbf{w}||^2 $$

Nhớ lại là nếu phân loại đúng thì $\xi_ n = 0$, với các điểm còn lại thì $\xi_ n = 1 - y_ n t_ n$. Hàm trên có thể viết lại thành:

$$ \sum_ {n=1}^N E_ {SV}(y_ n t_ n) + \lambda||\mathbf{w}||^2 $$

với $E_ {SV}(y_ n t_ n) = [1- y_ nt_ n]_ +$ gọi là hàm hinge error. Trong đó $[・]_ +$ để chỉ phần dương.

Đồ thị so sánh hinge error function với error function trong logsitic regression như sau:

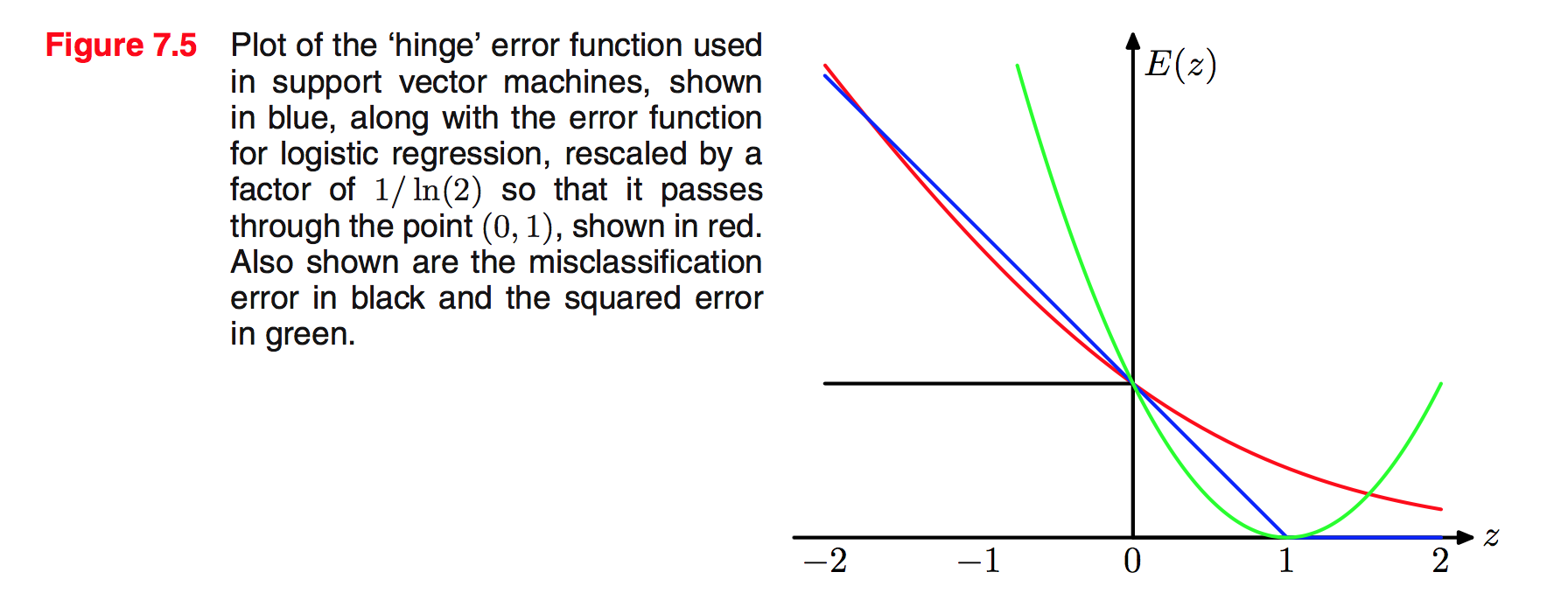
figure-7.5

Điểm khác biệt mấu chốt giữa logistic regression và SVM là:

  • Output của logistic regression là xác suất điểm đó rơi vào lớp nào.
  • Output của SVM là 1 giá trị cụ thể cho biết điểm đó rơi vào lớp nào (sparse solution).

7.1.3 Multiclass SVMs

Giả sử cần phân loại K > 2 classes.

  • one-versus-the-rest: Xây K cái SVMs độc lập với nhau, mỗi cái sẽ phân biệt 1 class với K-1 classes còn lại. Nhưng vấn đề ở chỗ K cái SVMs này độc lập với nhau nên không có gì đảm bảo để kết hợp các kết quả lại với nhau. Thêm nữa, data bị mất cân bằng (do negative data chiếm phần lớn) nên cũng làm việc train trở nên khó khăn.
  • one-versus-one: Xây $K(K-1)/2$ cái SVM phân biệt từng cặp classes với nhau. Kết quả cuối cùng là xem điểm đó rơi vào class nào nhiều nhất. Nhược điểm là phải train rất nhiều.