PRML - Chap 8: Graphical Models - 8.3
By Huy Van
$ \def\ci{\perp\!\!\!\perp} \def\given{\ | \ } \def\nci{\perp\!\!\!\perp\!\!\!\!\!\!/ \ } \def\zeroslash{0\!\!\!/} $
8.3 Markov Random Fields
Markov random field, còn gọi là Markov network hay undirected graphical model được biểu diễn bằng graph vô hướng.
8.3.1 Conditional independence properties
Sử dụng graph vô hướng sẽ dễ kiểm tra tính chất độc lập có điều kiện của 2 biến hơn (conditional independence property). Chú ý là chỉ giống với phép thử d-separation trong trường hợp không có hiện tượng ’explaining away'.
Ví dụ:
$$ A \ci B \given C $$
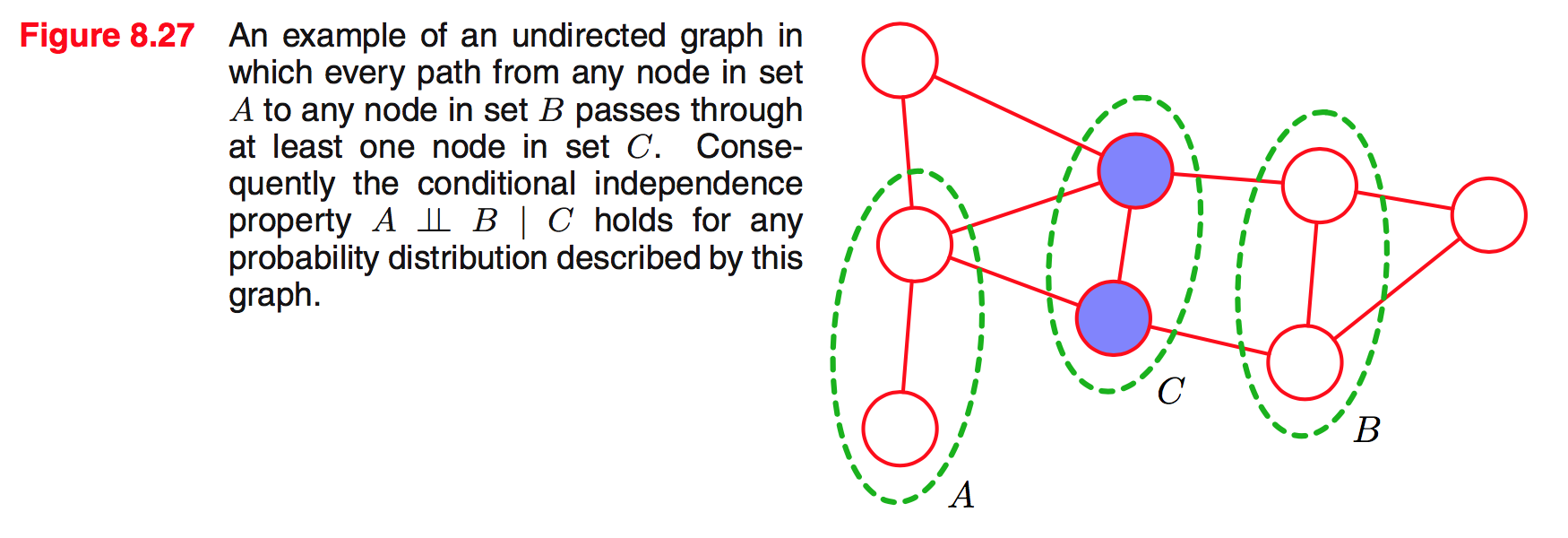
Trong ví dụ trên ta chỉ cần bỏ các nốt trong C ra khỏi graph thì sẽ thấy là không có đường đi (path) nào từ nốt thuộc A nối với nốt thuộc B. Trong trường hợp này, A và B độc lập với nhau với điều kiện C.
Markov blanket cũng được biểu diễn 1 cách đơn giản như sau:

8.3.2 Factorization properties
Nếu 2 nốt $x_ i$ và $x_ j$ không có đường nối với nhau thì 2 nốt này là độc lập với nhau với điều kiện tất cả các nốt còn lại của graph. Từ đó ta có thể phân tích thành nhân tử như sau:
$$ p(x_ i, x_ j | \mathbf{x}_ {\backslash \{i,j\}}) =p(x_ i | \mathbf{x}_ {\backslash \{i,j\}}) p(x_ j | \mathbf{x}_ {\backslash \{i,j\}}) $$
Clique: là 1 tập con các nốt của graph mà mỗi cặp nốt thuộc tập đó đều có 1 đường nối lẫn nhau. Hay nói cách khác là các nốt trong tập đó ‘fully connected’.
Maximal clique: là clique mà không thể thêm 1 nốt khác thuộc graph vào để tạo thành 1 clique.
Ví dụ:

Graph trên có 5 clique 2 nốt là $\{x_ 1, x_ 2 \}, \{x_ 2, x_ 3 \}, \{x_ 3, x_ 4 \}, \{x_ 4, x_ 2 \}, \{x_ 1, x_ 3 \}$, và 2 maximal clique là $\{x_ 1, x_ 2, x_ 3 \}, \{x_ 2, x_ 3 , x_ 4\}$. $\{x_ 1, x_ 2, x_ 3, x_ 4 \}$ không phải là 1 clique vì không có đường nối giữa $x_ 1$ và $x_ 4$.
Kí hiệu clique là $C$ và tập các biến trong clique đó là $\mathbf{x}_ C$.
Phân phối đồng thời của tất cả các nốt $p(\mathbf{x})$ có thể biểu diễn bằng tích của các hàm thế (potential function) $\psi_ C(\mathbf{x}_ C)$ của các maximal clique trong graph:
$$ p(\mathbf{x}) = \frac{1}{Z} \prod_ C \psi_ C (\mathbf{x}_ C) \tag{8.39} \label{eq:8.39} $$
Ở đây đại lượng $Z$, còn gọi là partition function, là hệ số chuẩn hoá để $p(\mathbf{x})$ ở trên đúng là 1 phân phối xác suất:
$$ Z = \sum_ {\mathbf{x}} \prod_ C \psi_ C (\mathbf{x}_ C) \tag{8.40} \label{eq:8.40} $$
Chúng ta chỉ xét hàm thế không âm ($\psi_ C (\mathbf{x}_ C) \ge 0$) thì sẽ đảm bảo được là $p(\mathbf{x}) \ge 0$.
Sự khác biệt lớn nhất đối với graph có hướng là ở đây đòi hỏi phải có hệ số chuẩn hoá. Cái này chính là hạn chế lớn vì tính toán $Z$ tỉ lệ hàm mũ với kích cỡ của model.
Để xem xét mối liên hệ giữa độc lập có điều kiện (conditional independence) và phân tích nhân tử (factorization) cho graph vô hướng, ta cần giới hạn hàm thế $\psi_ C (\mathbf{x}_ C)$ luôn dương. Với điều kiện này, định lý Hammersley-Clifford đã chỉ ra rằng việc phân tích tính độc lập có điều kiện dùng graph và phân tích nhân tử dùng công thức \eqref{eq:8.39} là như nhau.
Vì ta đã giới hạn hàm thế luôn dương nên để thuận tiện ta có thể chọn hàm mũ như sau:
$$ \psi_ C (\mathbf{x}_ C) = \exp\{-E(\mathbf{x}_ C)\} $$
Ở đây $E(\mathbf{x}_ C)$ gọi là hàm năng lượng (energy function), và biểu hiện hàm mũ này được gọi là phân phối Boltzmann. Vì phân phối đồng thời theo công thức \eqref{eq:8.39} được tính bằng tích của các hàm thế, nên năng lượng tổng hợp (total energy) sẽ là tổng năng lượng của các maximal clique. (Tự nhiên đưa ra khái niệm năng lượng tổng hợp chả hiểu đâu ra ☹️).
8.3.3 Illustration: Image de-noising
Ví dụ về ứng dụng loại bỏ nhiễu từ ảnh như hình dưới đây:

Có 1 cái ảnh gốc đen trắng không nhiễu mà mỗi pixel nó được biểu diễn bởi $x_ i \in \{-1, +1 \}$. Có thể hiểu là $+1$ là điểm đen, $-1$ là điểm trắng.
1 cái ảnh nhiễu sinh ra từ ảnh trên bằng cách lật dấu ngẫu nhiên khoảng 10% các điểm. Ảnh nhiễu này biểu diễn bởi $y_ i \in \{-1, +1 \}$.
Bài toán đặt ra là cho ảnh nhiễu, làm thế nào để phục hồi được ảnh gốc.
Vì nhiễu là nhỏ nên có thể coi $x_ i$ và $y_ i$ có mối tương quan chặt (strong correlation). Thêm nữa ta cũng thấy là các pixel liền kề $x_ i$ và $x_ j$ cũng có mối tương quan chặt. Những kiến thức biết trước này (prior knowledge) có thể được biểu diễn bằng mô hình Markov random filed có đồ thị vô hướng như sau:

Graph này có 2 loại clique như sau:
Clique dạng $\{x_ i, y_ i \}$. Ta chọn hàm năng lượng biểu diễn mối tương quan giữa $x_ i$ và $y_ i$ là $-\eta x_ i y_ i$, với $\eta$ là 1 hệ số dương. Hàm này đúng tính chất thế năng nghĩa là năng lượng thấp (nghĩa là xác suất cao) khi $x_ i, y_ i$ có cùng dấu, và năng lượng cao (nghĩa là xác suất thấp) khi chúng trái dấu.
Clique dạng $\{x_ i, x_ j \}$ cho các pixel cạnh nhau. Tương tự ta cũng chọn được hàm năng lượng $-\beta x_ i x_ j$, với $\beta$ là 1 hệ số dương.
Vì hàm thế là 1 hàm bất kỳ nên ta có thể chọn năng lượng tổng hợp như sau:
$$ E(\mathbf{x},\mathbf{y}) = h\sum_ i x_ i - \beta \sum_ {\{i,j\}} x_ i x_ j - \eta\sum_ i x_ i y_ i $$
Đại lượng $h\sum_ i x_ i$ đóng vai trò như là phân phối prior đối với $x_ i$.
Xác suất đồng thời giữa $\mathbf{x}$ và $\mathbf{y}$ sẽ thành:
$$ p(\mathbf{x}, \mathbf{y}) = \frac{1}{Z} \exp \{ -E(\mathbf{x},\mathbf{y}) \} $$
Mục tiêu của ta là giá trị lớn nhất của $p(\mathbf{x}|\mathbf{y})$ (cũng tương đương với tìm giá trị lớn nhất của $p(\mathbf{x},\mathbf{y})$?). Nghĩa là đồng nghĩa với tìm giá trị nhỏ nhất của hàm năng lượng.
Để giải bài toán này ta có thể sử dụng kỹ thuật tên là iterated conditional modes hay ICM. Cái này là ứng dụng của coordinate-wise gradient ascent. Tư tưởng của kỹ thuật này là:
- Khởi tạo $\{x_ i\}$ bằng $x_ i = y_ i$ với mọi $i$.
- Xét 1 nốt $x_ j$ tại 1 thời điểm, tính năng lượng tổng hợp cho 2 trạng thái $x_ j = +1$ và $x_ j = -1$, trong khi giữ nguyên giá trị của tất cả các nốt còn lại. Gán $x_ j$ cho trạng thái có năng lượng nhỏ hơn. Việc này luôn làm cho năng lượng tổng hợp nhỏ đi.
- Việc chọn $x_ j$ có thể bằng cách quét lần lượt hay chọn bất kỳ. Bước này cứ thế lặp lại cho đến khi quét hết 1 lượt mà không có sự thay đổi nào diễn ra. Kết quả sẽ hội tụ về 1 cái local minimum của năng lượng (hay local maximum của xác xuất đồng thời).
8.3.4 Relation to directed graphs
Xét ví dụ đơn giản như sau:

(Hình này in sai ở (b) $x_ N$ và $x_ {N-1}$ bị ngược).
- Graph có hướng:
$$ p(\mathbf{x}) = p(x_ 1)p(x_ 2|x_ 1)p(x_ 3|x_ 2)\ldots p(x_ N|x_ {N-1}) $$
- Graph vô hướng:
$$ p(\mathbf{x}) = \frac{1}{Z} \psi_ {1,2}(x_ 1, x_ 2)\psi_ {2,3}(x_ 2, x_ 3)\ldots \psi_ {N-1,N}(x_ {N-1}, x_ N) $$
Dễ dàng cho 2 cái này bằng nhau bằng việc:
$$ \begin{align} \psi_ {1,2}(x_ 1, x_ 2) & = p(x_ 1)p(x_ 2| x_ 1) \\ \psi_ {2,3}(x_ 2, x_ 3) & = p(x_ 2| x_ 1) \\ & \vdots \\ \psi_ {N-1,N}(x_ {N-1}, x_ N) & = p(x_ N| x_ {N-1}) \end{align} $$
Chú ý là ở đây partition function $Z=1$.
Tổng quát hoá chuyển từ graph có hướng sang vô hướng:
- Với nốt chỉ có 1 nốt mẹ, đơn giản chỉ cần chuyển đường có hướng thành vô hướng.
- Với nốt có nhiều nốt mẹ, cần vẽ thêm đường nối tất cả các mẹ với nhau. Quá trình này gọi là ‘marrying the parents’ hay moralization. Graph vô hướng thu được gọi là moral graph.
- Khởi tạo các hàm thế của moral graph bằng 1. Sau đó lấy mỗi nhân tử xác suất có điều kiện của graph có hướng gốc rồi nhân với 1 trong các hàm thế. Sẽ luôn tồn tại ít nhất 1 maximal clique chứa tất cả các biến trong nhân tử như là kết quả của bước moralization. Chú ý là trong mọi trường hợp $Z=1$.
Ví dụ:
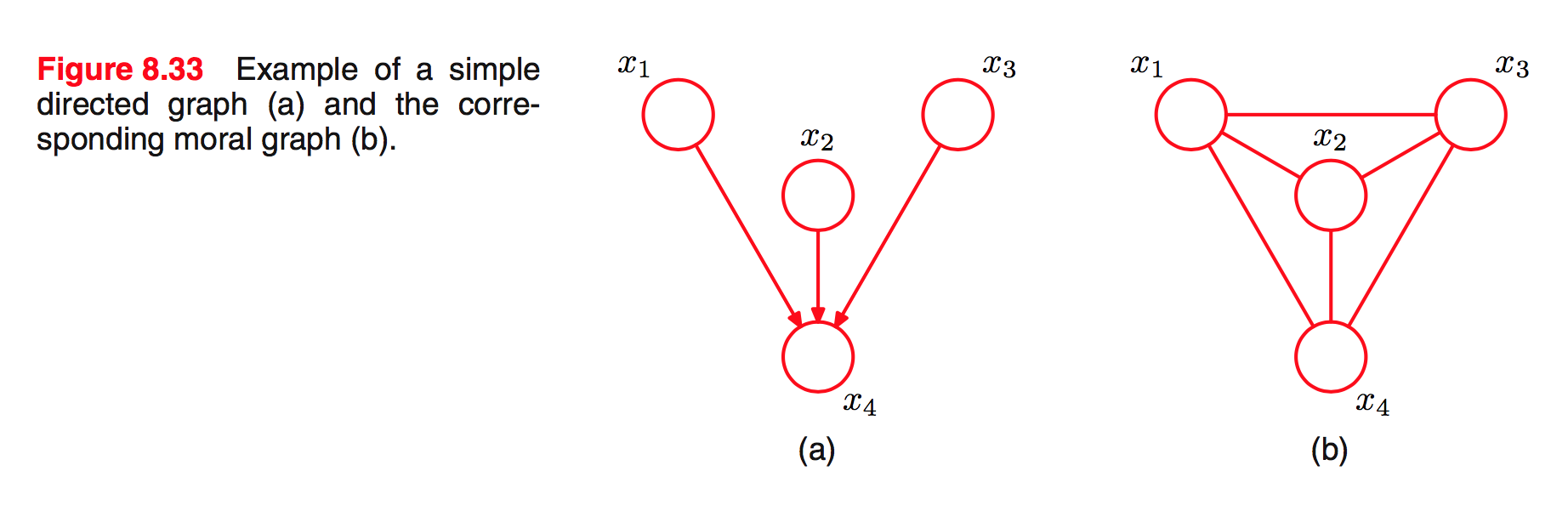
Ngược lại chuyển từ graph vô hướng sang có hướng rất ít khi gặp trong thực tế vì vướng phải vấn đề chuẩn hoá.
Để ý là trong việc chuyển từ graph có hướng sang vô hướng, ta đã loại bỏ 1 vài mối quan hệ độc lập có điều kiện trong graph. Quá trình moralization thêm tối thiểu số đường nối nên giữ được tối đa số mối quan hệ độc lập có điều kiện.
1 vài định nghĩa không biết dịch thế nào:
- D map (viết tắt của ‘dependency map’): a graph is said to be a D map of a distribution if every conditional independence statement satisfied by the distribution is reflected in the graph.
- I map (viết tắt của ‘independence map’): if every conditional independence statement implied by a graph is satisfied by a specific distribution, then the graph is said to be an I map of that distribution.
- Perfect map: vừa là D map vừa là I map.
Xét tập các phân phối mà mỗi phân phối đều biểu diễn được bằng 1 perfect map. Tập này khác với tập mà mỗi phân phối đều biểu diễn được bằng 1 graph có hướng mà graph đó là perfect map. Tương tự với graph vô hướng. Mối tương quan này được biểu diễn bằng sơ đồ Venn như sau:

Ví dụ về graph có hướng mà là 1 perfect map cho 1 phân phối thoả mãn tính chất độc lập có điều kiện $A \ci B \given \zeroslash $ và $A \nci B \given C$. Không tồn tại graph vô hướng nào đối với 3 biến này mà là perfect map.

Ví dụ về 1 graph vô hướng với 4 biến. Graph này thể hiện tính chất $A \nci B \given \zeroslash, C \ci D \given A \cup B, A \ci B \given C \cup D$. Không tồn tại graph có hướng nào giữa 4 biến này mà biểu diễn được các tính chất trên.
